Le son est une onde mécanique progressive sinusoïdale. Une onde mécanique est la propagation d'une perturbation dans un milieu matériel solide, liquide ou gazeux. Le son est une d'onde particulière, puisqu'il s'agit d'une onde longitudinale où la déformation du milieu dans lequel elle se propage s'effectue parallèlement à son déplacement.
Cette onde, le son, ne peut pas se propager dans le vide, en l' absence de matière. Toutes les ondes mécaniques ont une vitesse qui leur est propre. Cette vitesse de déplacement, appelée célérité pour les ondes est susceptible de changer, selon la rigidité du milieu dans lequel elle se propage.
On peut écrire :
![]()
C : Célérité en m/s
d : distance parcourue en mètres
t : durée en secondes
Les sons que perçoit l' homme se propagent généralement dans l'air, et ce bien qu'il soit capable d'en percevoir dans l'eau. La "rigidité" de l'air est susceptible de changer selon certains paramètres, la température et la pression. On peut calculer la célérité du son dans l'air en fonction de la température grâce à la relation suivante:
![]()
T : température en Kelvins.
Ainsi a 20°C soit 293K on calcule la célérité du son :
![]()
Dans l'eau, le son se déplace a 1460 m/s et dans l'acier à 5500 m/s.
Le son met 3 secondes pour parcourir 1 km: si l'on entend le tonnerre 6 s après avoir vu l'éclair, la foudre est tombée à 2 km.
Toute onde sinusoïdale possède des caractéristiques remarquables qui lui sont propres.
La période : Il s'agit de la plus petite durée mise par l'onde pour effectuer un motif. Dans le cas du son, c'est ce qui caractérise la hauteur du son que l'on perçoit.
La longueur d'onde : elle est notée ![]() et s'exprime en mètres. Il s'agit de la distance parcourue par l'onde en une période.
et s'exprime en mètres. Il s'agit de la distance parcourue par l'onde en une période.
Entre la période et la longueur d'onde existe donc la relation suivante :
![]()
La fréquence f est le nombre de périodes par seconde. Elle s'exprime en hertz (symbole Hz), 1 Hz = 1 s -1
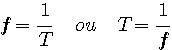
et donc :
![]()
La fréquence d'une onde sonore définit la hauteur du son, ce qui le rend aigu ou grave. L'Homme entend en moyenne les sons de fréquences comprises entre 20 Hz (sons graves) et 20 000 Hz (sons aigus). On ne perçoit plus les sons très aigus au delà d'une certaine fréquence et inversement, on ne perçoit pas non plus les sons graves en dessous d'une certaine fréquence. Avec l'âge, ce domaine se rétrécit et est propre à chacun. Les chauve-souris n'entendent, par exemple, que les sons de fréquence supérieure à 1 000Hz. Le chien et le dauphin entendent également les ultrasons, qui ont des fréquences supérieures à 20kHz. Au dessous de 20Hz on parle d'infrasons qui ne sont plus des sons à proprement parler.
La tonalité du téléphone ou un diapason donnent le la3 (le la du 3ème octave sur une clavier) de fréquence 440 Hz. D'un octave au suivant, la fréquence est doublée: ainsi le la4 a une fréquence de 880 Hz.
Une onde sonore est définie non seulement par sa fréquence mais aussi par son amplitude. L'intensité d'un son, son « volume » est liée à l'amplitude de l'onde acoustique correspondante. Cette dernière représente en fait une mesure du déplacement des molécules d'air. Plus l'amplitude de l'onde sera grande, plus les molécules d'air frapperont avec force la membrane de l'oreille, et donc plus le son paraîtra fort. L'intensité d'une onde acoustique peut être obtenue de différentes manières. Par exemple, on peut mesurer la distance du déplacement relatif des molécules d'air, ou bien encore la différence de pression qui s'opère au cours des dilatations et compressions successives de l'air. On peut également la calculer en mesurant l'énergie mise en jeu par les vibrations sonores. La relation entre la sensation sonore et l'énergie sonore n'est pas simple. La sensation sonore n'est pas proportionnelle à l'énergie sonore reçue par l'oreille ( si c'était le cas, la sensation provoquée par le bruit du tonnerre serait insupportable). Il existe un certain nombre de modèles mathématiques qui permettent de quantifier le niveau sonore et d'étudier le comportement du son dans certains cas.
Schéma récapitulatif :
T : la période de l'onde
A : l'amplitude de l'onde
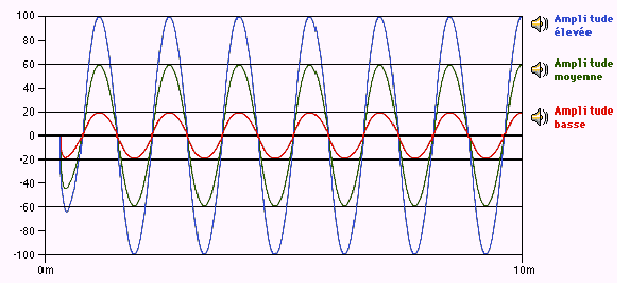
On distingue différentes notions pour mesurer l'amplitude d'un son :
La puissance acoustique est associée à une notion physique. Il s'agit de l'énergie transportée par l'onde sonore par unité de temps et de surface. Elle s'exprime en Watt par mètre carré (W.m -2 ) , cependant on préférera utiliser le niveau acoustique pour des raison pratiques.
Il s'agit de la mesure relative de la puissance acoustique, notée Li (Level intensity) et est exprimée en décibels (dB). Comme la sensation auditive n'est pas linéaire mais varie comme le logarithme de l'excitation, on utilise généralement cette définition.
On a donc :
LI(dB) = 10.log(I/Io) avec I en W.m -2 .
Io est le niveau de référence au seuil d'audibilité à 1000 Hz et vaut Io = 10 -12 W.m -2 .
Nb : (en acoustique sous-marine Io = 0,66.10 -18 W.m -2 )
On utilise parfois une définition exprimée en fonction de la pression, notée Lp (pour, Level pressure, en anglais) et est également exprimée en décibels.
Lp = 20.log( Pe/Po ) avec p o = 2.10 -5 Pa (pression acoustique de référence, seuil d'audibilité à 1000 Hz).
Pa : Pascal, Une force de 1 newton exercée sur une surface de 1 m² correspond à une pression de 1 Pa.
L'intensité sonore diminue avec l'inverse du carré de la distance à la source du son. Par exemple, si on s'éloigne de 200 mètres d'une source sonore, le niveau sonore sera normalement de un quart de celui à 100 m de distance. En doublant la distance, le niveau en dB sera divisé par 6.
L'échelle des dB est une échelle dite logarithmique, ou relative, ce qui signifie qu'un doublement de la pression sonore, de l'énergie du son, implique un accroissement de l'indice par approximativement 3. Un niveau sonore de 100 dB contient donc deux fois plus d'énergie qu'un niveau sonore de 97 dB. Si l'on mesure le niveau sonore de cette façon, c'est que nos oreilles (et notre cerveau) perçoivent le son en termes du logarithmique de la pression sonore, plutôt qu'en termes de la pression sonore en elle-même.
Exemple : 40 dB et 40 dB ne donnent pas 80 dB mais 43 dB. 70 dB et 70 dB ne donnent pas 140 dB mais 73 dB.
Le résultat de l'addition de deux niveaux sonores identiques n'est pas un niveau sonore double mais le niveau sonore augmenté de 3 décibels :
Demonstration :
Les niveaux sonores se composent donc. Le bruit augmente de 3 dB chaque fois que son énergie double. Une conversation normale correspond approximativementà un niveau de 40dB :
Exemple, L'addition des niveaux sonores des élèves qui parlent en classe.. !
1 élève |
|
40 dB |
2 élèves |
|
43 dB |
3 élèves |
|
45 dB |
4 élèves |
|
46 dB |
Une classe 35 élèves : |
|
55.5 dB |
Soit un gain de 15.5 dB… ! (d'où les maux de crâne à la fin de la journée..)
Enfin, le son est non seulement défini par sa hauteur et son volume, mais l'est également par son timbre. Nous entendons tous le timbre de différents sons, ce qui fait que nous pouvons faire la différence entre une même note de piano ou de violon par exemple. Si on joue le La3 sur un diapason, un piano, ou un violon, à volume identique, ces trois sons ont la même fréquence et la même amplitude, mais possèdent un timbre nettement différent. De ces trois sources sonores, le son le plus pur est celui émis par le diapason, car il est constitué presque uniquement de vibrations ayant une fréquence de 440 Hz. En revanche, le la3 produit par un piano ou un violon se compose d'une vibration principale de 440 Hz, appelée la fondamentale, à laquelle se superposent d'autres vibrations, dont les fréquences sont des multiples entiers de la fréquence fondamentale. Ces vibrations annexes sont appelées partielles harmoniques, ou plus simplement harmoniques, et leurs intensités déterminent le timbre de la note. D'autres vibrations peuvent encore constituer le son, les partiels. Ces vibrations sont composantes d'un son complexe et leur fréquence de vibration n'est pas nécessairement dans un rapport simple avec la fondamentale. Un son est donc la superposition complexe de diverses ondes sonores et n'existe jamais naturellement à l'état d'une seule et unique vibration.